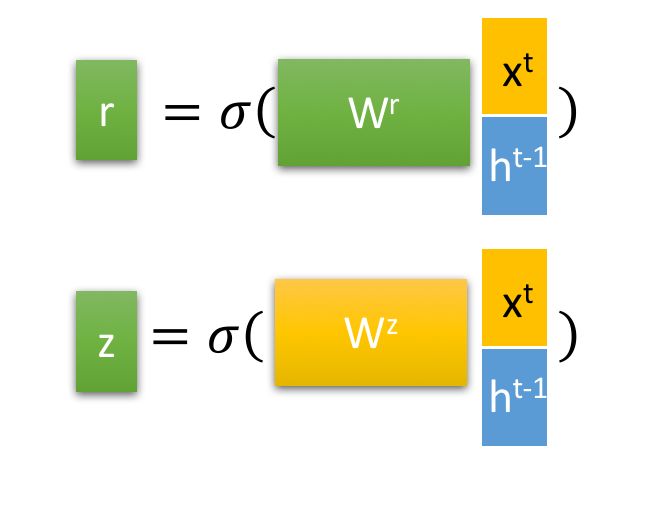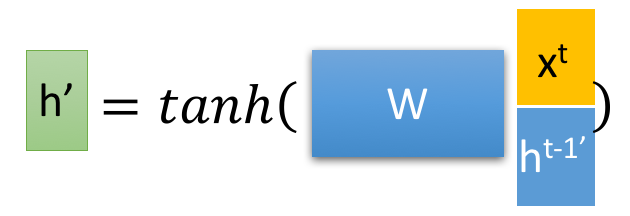ML学到的一些杂项

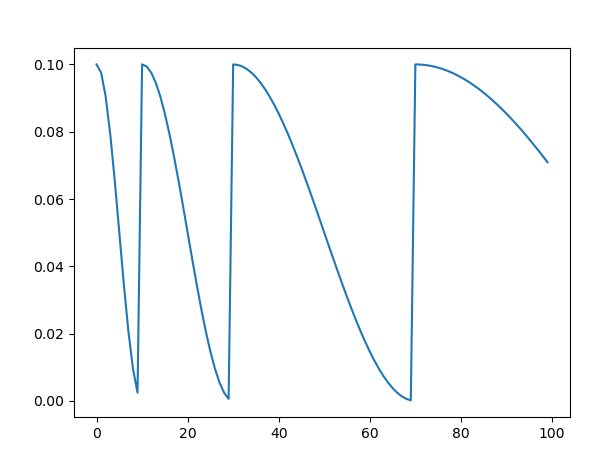
余弦退火函数

from torch.optim.lr_scheduler import CosineAnnealingLR,CosineAnnealingWarmRestarts,StepLR

scheduler = CosineAnnealingWarmRestarts(optimizer,T_0=2,T_mult=2)

上古先贤的智慧

如果 T_mult=1 就在 T_0,2T_0,...,NT_0 取得 lr 最大值

否则，在 T_0+n*T_mult , n in [0,N] 取得 lr 最大值

BN Batch Normalization

名词：convariate shift 协变量便宜，由于网络是 deep 的，每一层的输出变化会导致下一层输入数据的偏移，因此后面的网络需要不断适应这个变化，导致训练效率降低。

Internal Covariate Shift=ICS

解决方式：

白化（Whitening）

白化（Whitening）是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换，进而达到以下两个目的：

使得输入特征分布具有相同的均值与方差。其中PCA白化保证了所有特征分布均值为0，方差为1；而ZCA白化则保证了所有特征分布均值为0，方差相同；
去除特征之间的相关性。
通过白化操作，我们可以减缓ICS的问题，进而固定了每一层网络输入分布，加速网络训练过程的收敛（LeCun et al.,1998b；Wiesler&Ney,2011）。

该段摘抄自知乎

BN

BN可以解决数据分布的问题，使后面的网络不用根据前面的数据大幅度调整，并且对参数的适应力更强，避免模型 divergence 。

此外，BN可以用 sigmoid,tanh 并且缓解梯度消失。

BN也可以取代一部分 dropout 的功能

无偏估计

知乎

$\color{RED}\text{注意：文中广告与本人无关}$

Xavier初始化

RNN+LSTM+GRU

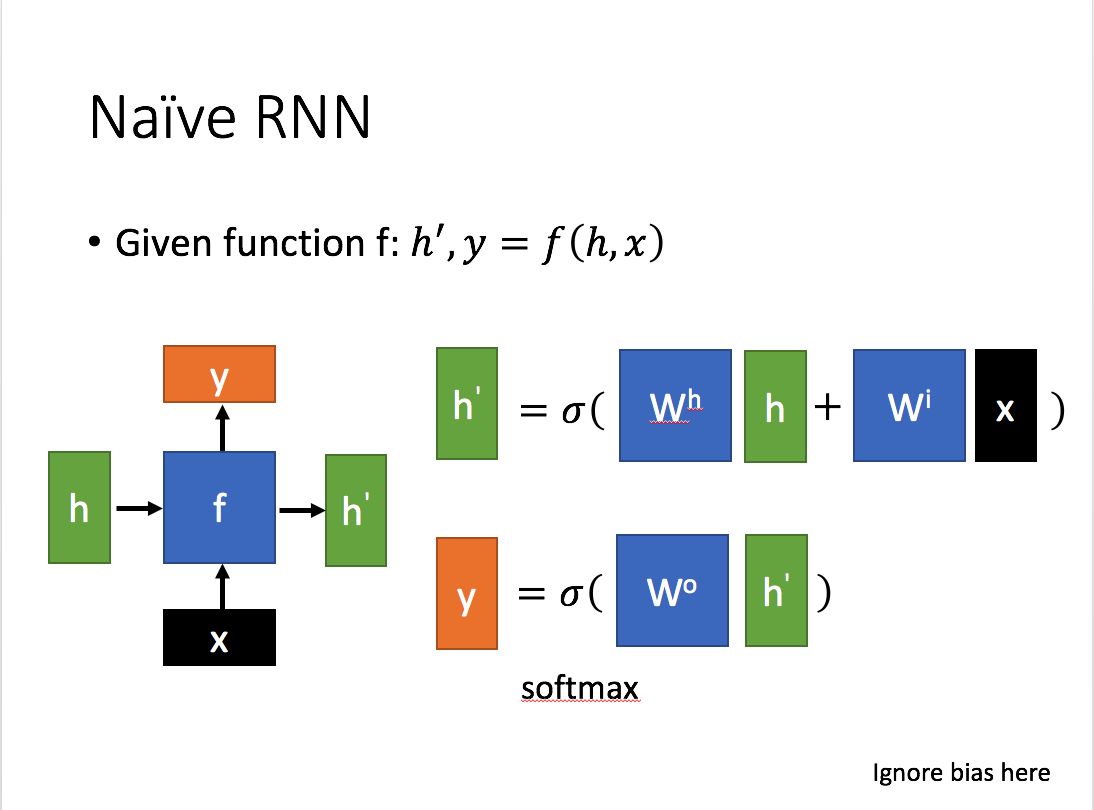
传统的 RNN 结构如左图所示， $h^{t-1}$ 和 $x^t$ 共同决定了 $y^t$ ，并且隐藏层也决定了 $h^t$ 。

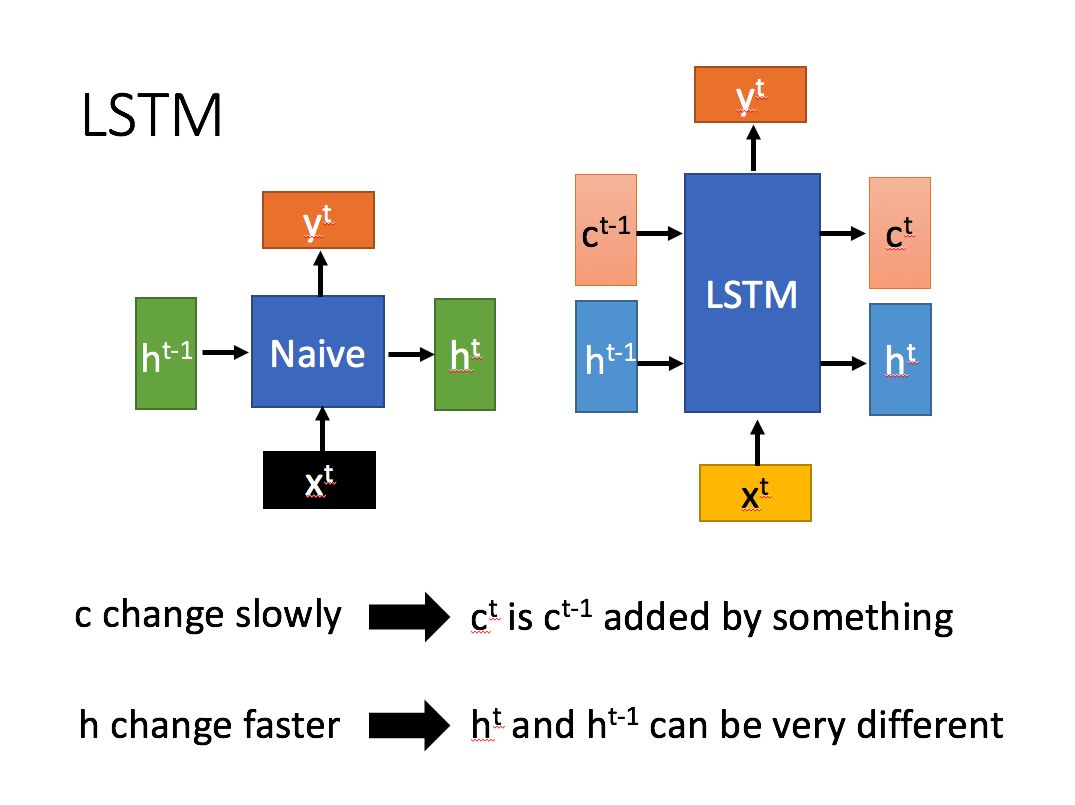
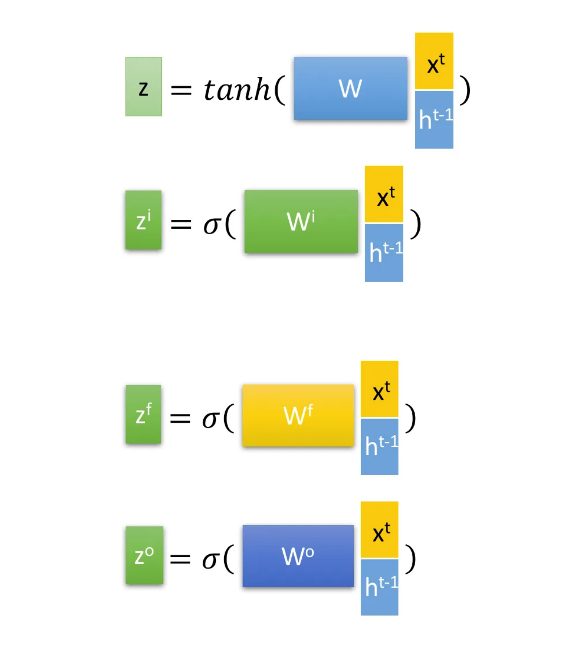
LSTM 拥有了两个类似于普通 RNN 的参数 $h,c$ ，其中 $h$ 前后变化幅度大而 $c$ 变化较为平缓

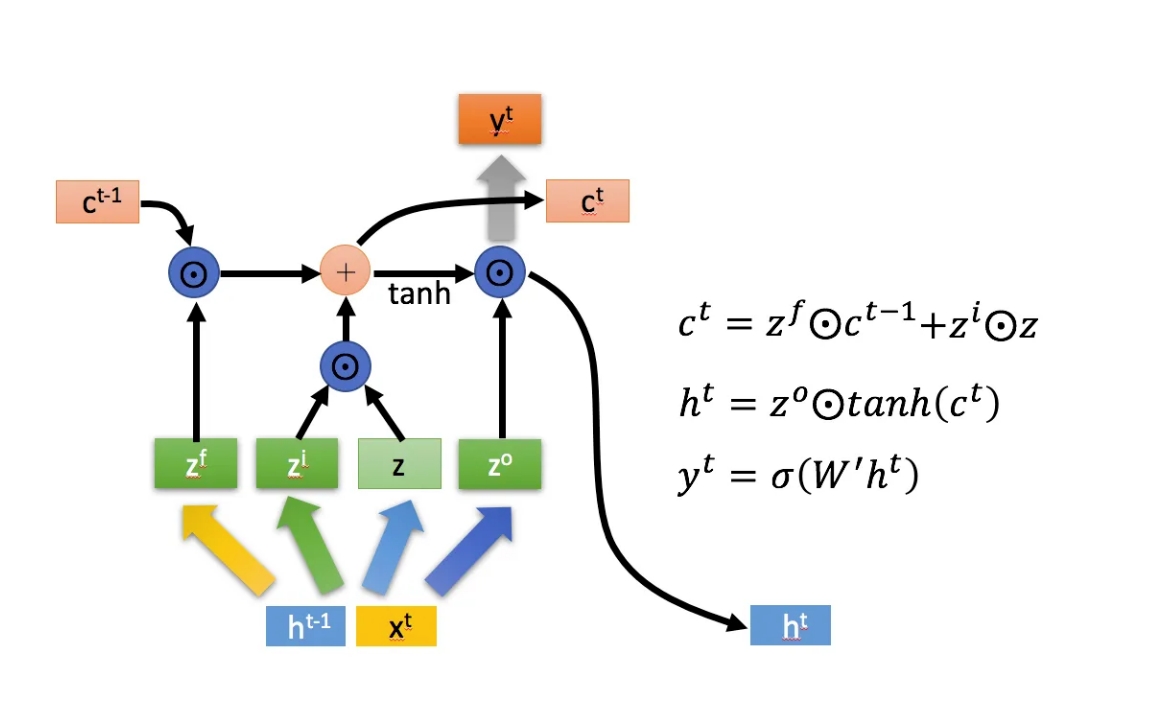
这几个参数的计算方式如下， $\odot$ 为 $\text{Hardmard}$ 积 ，$\oplus$ 是矩阵加， $z^i,z^f,z^o$ 是门控,函数是 $ \text{sigmoid} $ 。

RNN 并不适用于 BN,但是有Layer Normalization（LN）。

神仙的LSTM博客写得比这篇垃圾高明到不知到哪里去了

但是 LSTM 运算消耗太大了，于是考虑简化，保持 Naive 的 RNN 外部架构不变，更改一下内部架构

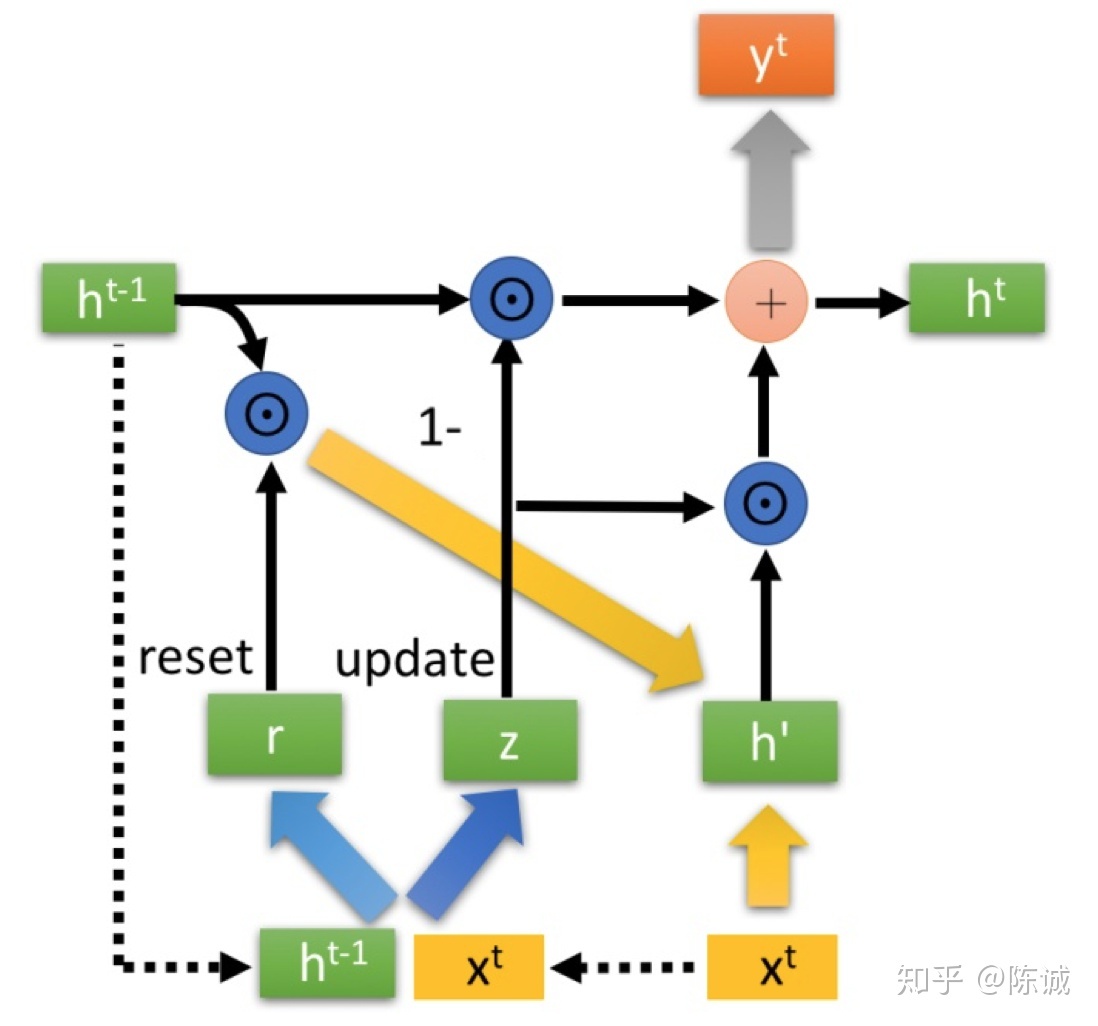
内部计算架构如图所示

$r,z$ 是门控，函数是 $ \text{sigmoid} $ 。

LSTM 流程

当输入一个数据，首先会判断是否忘记，也就是计算 $z^{f=forget}$，来决定要忘 $c^{t-1}$ 的哪些内容，之后会判断 $z^{i=information}$ 来决定记住哪些内容，最后是决定输出，也就是计算 $z^{o=output}$ ，并且也利用它改变一下 $h^t$ 的值

GRU

GRU 把记忆和一样同步进行（更新记忆）阶段

$h^t=(1-z)\odot h^{t-1}+z\odot h'$

$z$ 越大，记忆的也就越多，反之就越小。记忆指的是记忆$h'$

$h'=r \odot h^{t-1}$

Layer Normalization (LN)

normalization: 一组数据删除均值然后除以方差即可

相当于把数据转置一下然后 bn 然后转置回来

Attention

注意力机制

（图源见水印）

对于较长的文本， Seq2Seq 效果不太理想（我没试验过 LSTM or GRU ）

一个解决办法是给 seq2seq 引入 Attention 机制

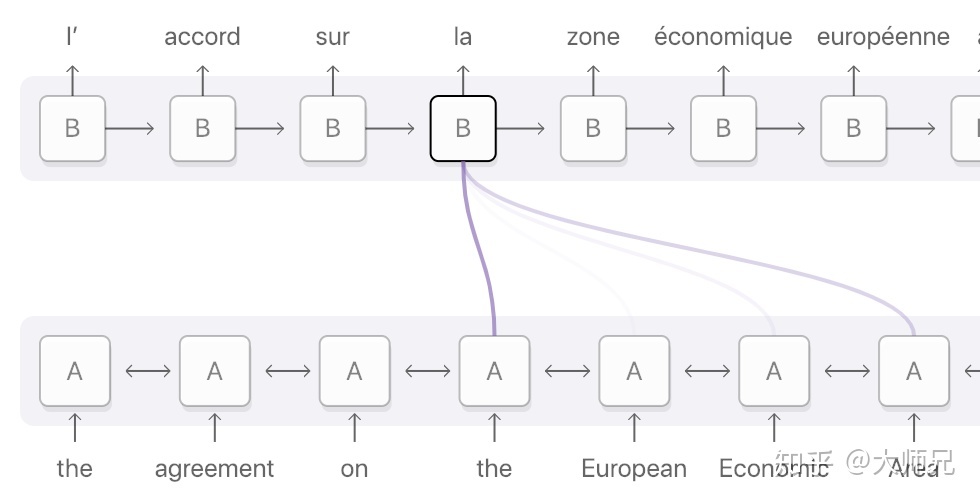
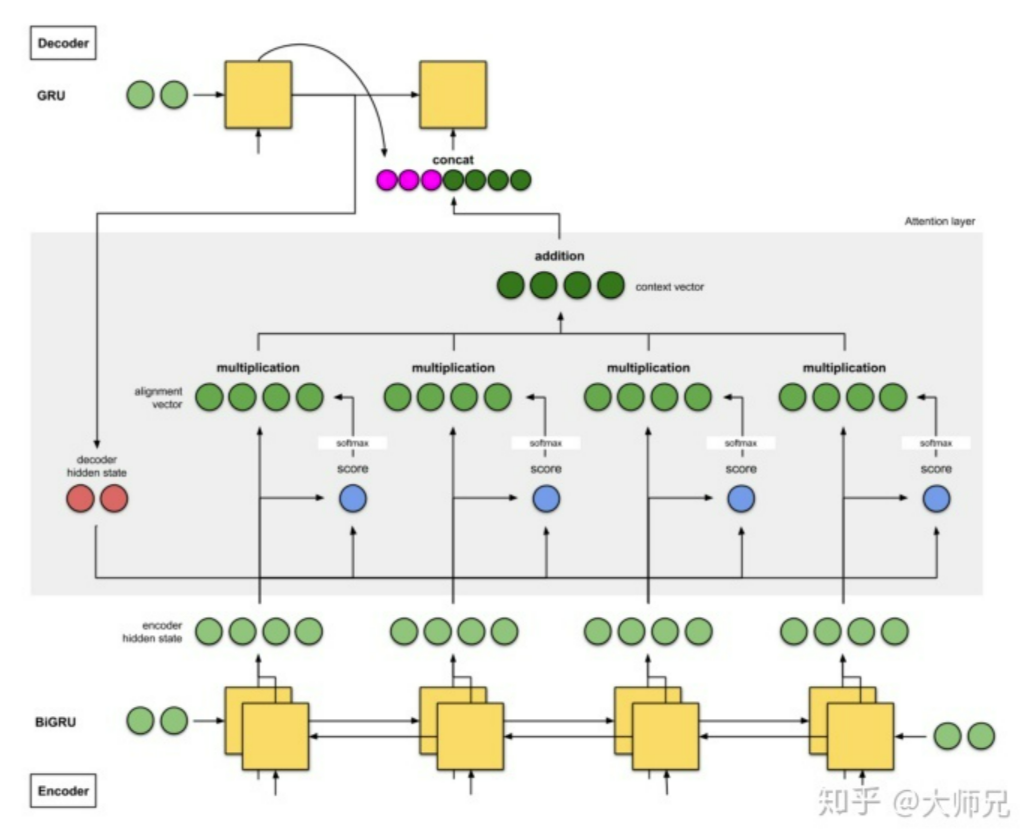
Attention 模型学习了 enc 和 dec 的对齐方式

引入的结果如下

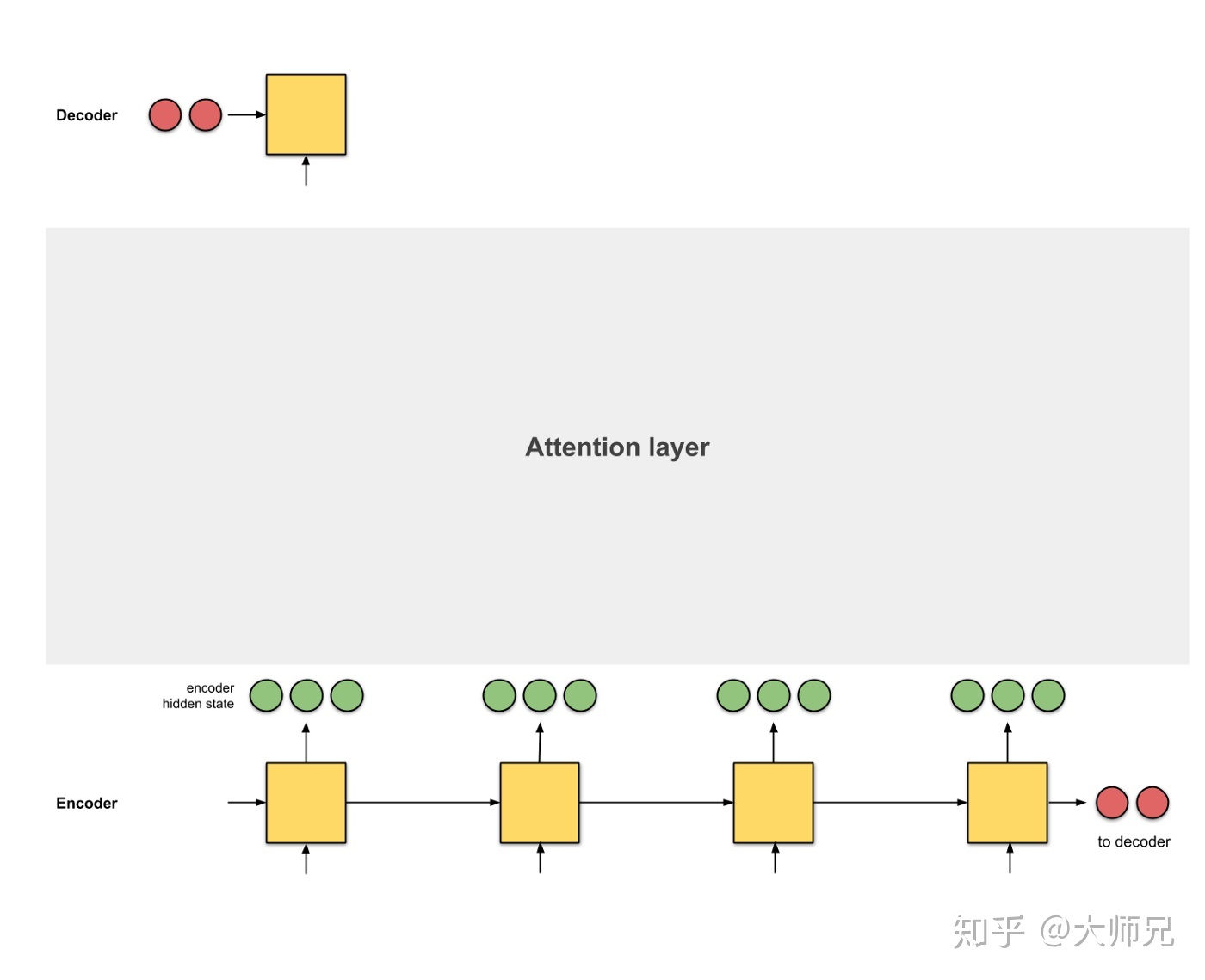
Attention 机制包含以下四个步骤

1 生成编码节点，根据前一个时间片的输出产生 hidden state

2 为每一个 hidden state 计算 score

3 利用 softmax 归一化 score

4 将其与 hidden state 点乘

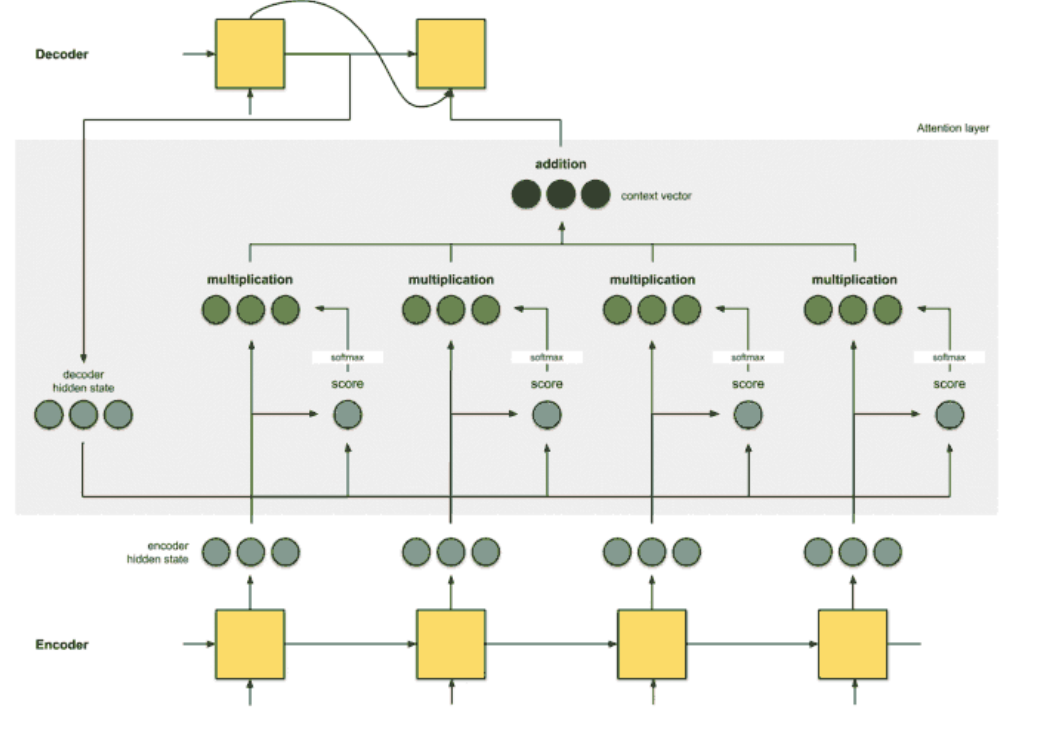
引入 ttention 的 Seq2Seq 还需要的步骤是

加和，得到编码器的特征向量（图中addition），然后提供给 dec

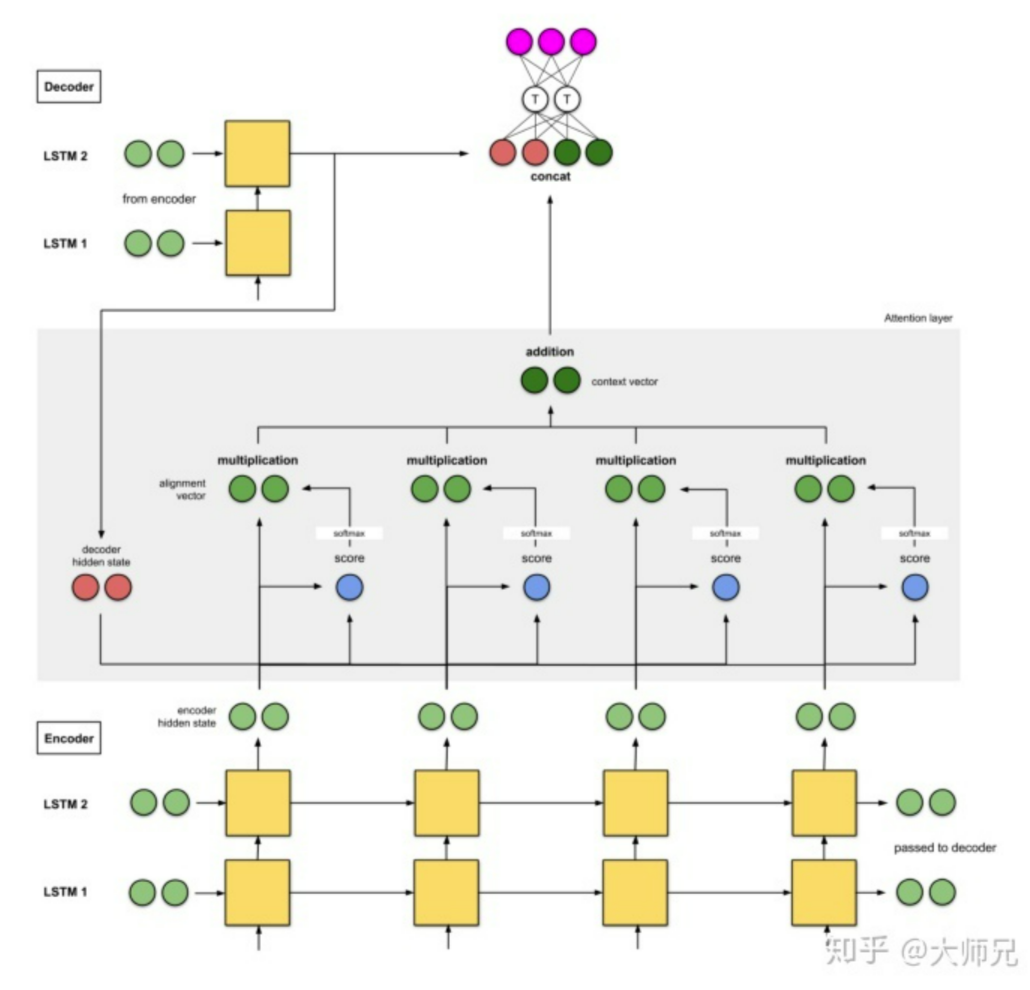
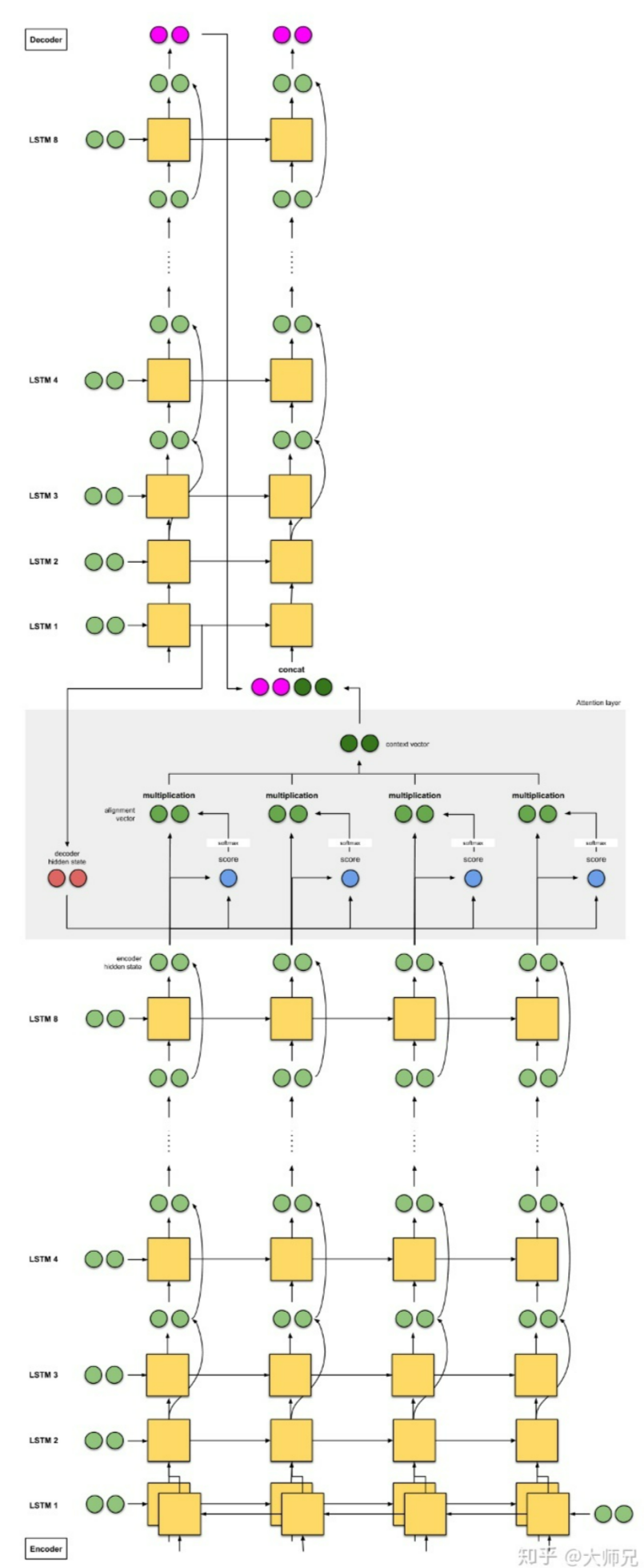
除了最基础的 RNN ，还有以下的改进版

配置虚拟环境

血的教训！

首先pip install virtualenv

然后打开 activate.ps1