Link Analysis: PageRank (Graph as Matrix)

由于每章都有很多芝士点，所以我打算改成一章一章来了

前言

用邻接矩阵的形式来看这张图

目标

定义图上节点的重要性，比如互联网上每个网站的重要性（node:网站,edge=hyperlink，directed）

有些情况暂时不需要考虑：

1.pages created on the fly 大概是随手生成的

2.dark matter 有密码这样的

应用场景

网页内，网页间，引用，百科等。

PageRank

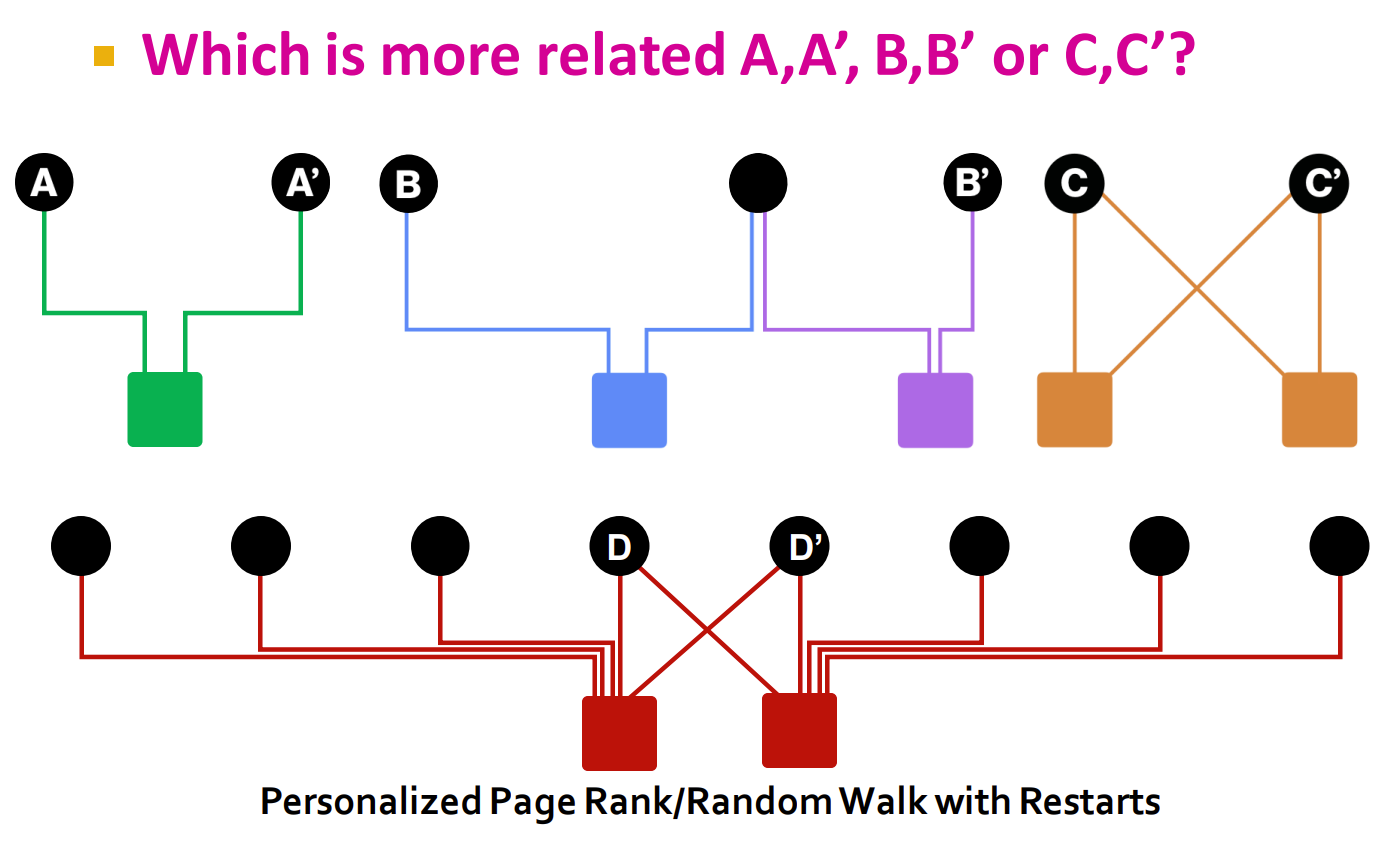
主要是三种 PageRank , Personalized PageRank (PPR) 和 Random Walk with Restarts

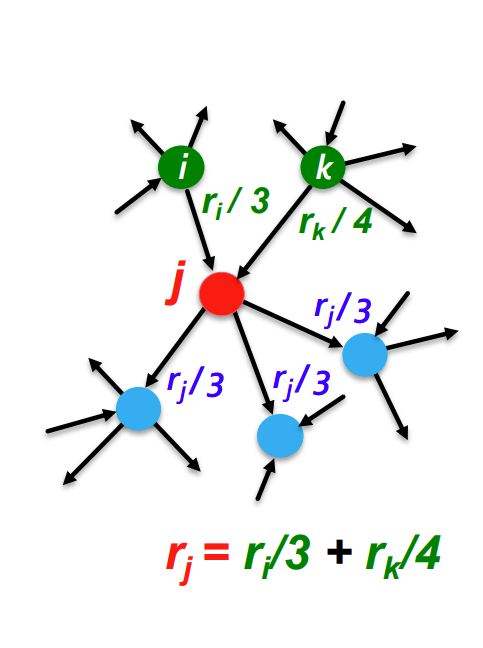
方法就是把超链接视为权重，如果自己被重要的网站挂了重要的网站（权重）有一个指向该网站的超链接，那显然这个网站权重也很高，我们通过这个方式计算每个网站的权重，显然这是一个递归问题。

计算权重

假设第 ii 点权重为 rir_i ， 度数为 did_i （出度） ,我们可以让 ii 连接的每一个节点的权重加上 ridi\frac{r_i}{d_i}

zbj76K.png

换句话说，我们想要这样迭代

rj=∑i→jridir_j=\sum_{i\to j}\limits\frac{r_i}{d_i}

显然，这样的转移可以写成一个矩阵的形式。

聪明的你一定想到了高斯消元，然后经典发问：我这个跑了一天怎么还没跑出来啊

现在我们定义一个向量 rr ,其中 rir_i 表示 ii 的重要性，并且满足∑iri=1\sum_{i}\limits r_i = 1

我们在构造一个矩阵，使得 Mj,i=1diif  i→jM_{j,i} = \frac{1}{d_i} \text{if}~~i \to j

此时转移可以写为 r=M×rr=M\times r，这是一个迭代过程，假设现在为 tt 时刻，有p(t+1)=M×p(t)p(t+1)=M\times p(t)

这个形式形如 λc=Ac\lambda c=Ac

如果 rr 经过多次迭代后，满足式子 1×r=M×r1\times r=M\times r 那么我们就没必要继续算了

实际上我们可以认为当 ∑i∣rit+1−rit∣<ϵ\sum_{i}\limits|r_i^{t+1}-r_i^t| < \epsilon 时，收敛（convergence）

幂迭代(power iterations)

首先初始化，r(0)=[1N,1N,1N,...,1N]r^{(0)}=[\frac{1}{N},\frac{1}{N},\frac{1}{N},...,\frac{1}{N}]

然后迭代，rt+1=M⋅r(t)r^{t+1} =M \cdot r^{(t)} 直到收敛

一般来说，到50次左右就可差不多了

特殊情况

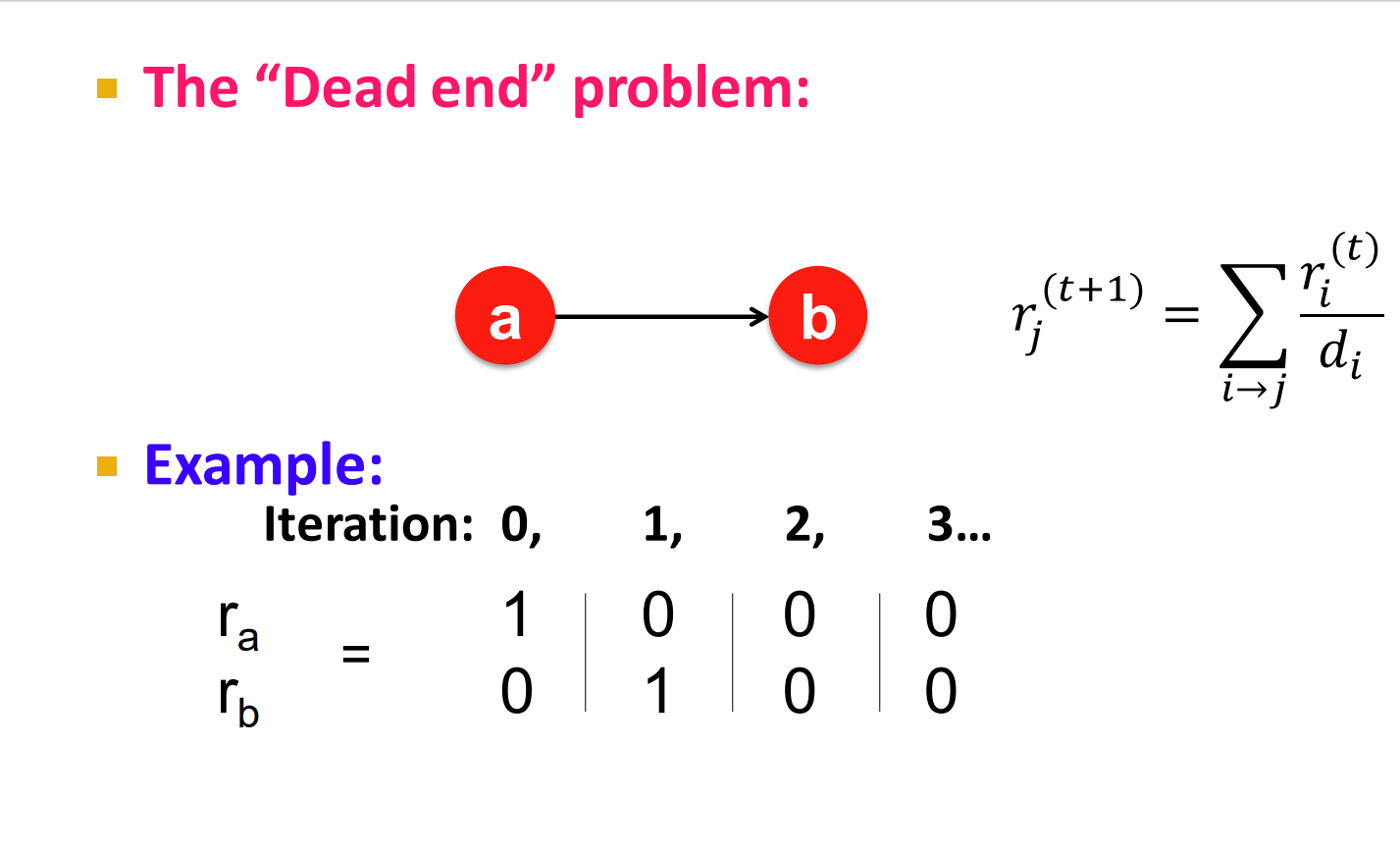
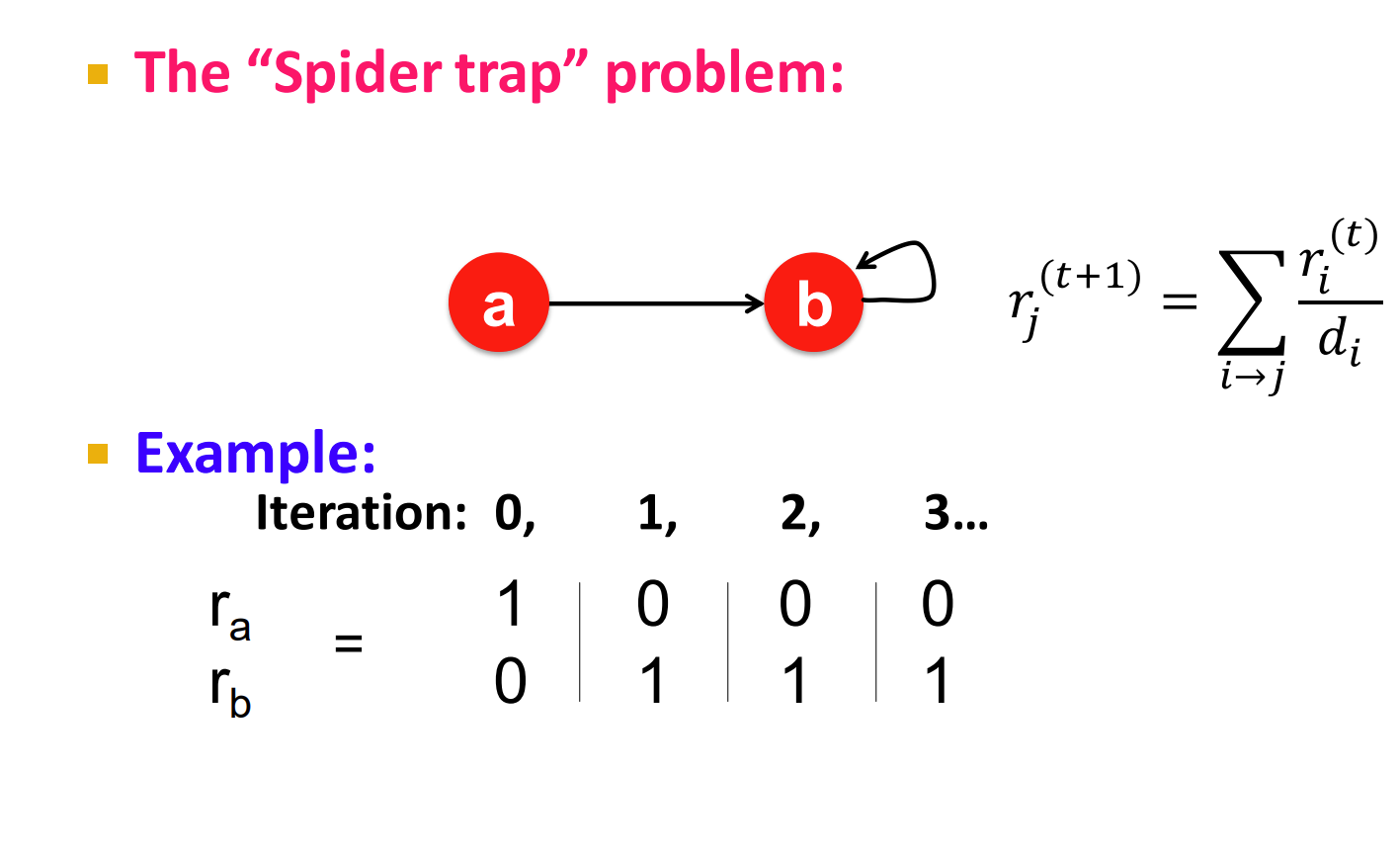
然而，这么做的话，有两个特殊情况无法解决

1.死点 dead ends 出度为0的点，这样之后整张图权重会变成0

2.Spider traps,all out-links are within the group，大概的意思就是说出现了一个scc，然后这个scc吃满了所有的重要性。

zqZW7R.png
zqZRB9.png

解决这个问题

此时我们跳不出去是吧，我们设定一个概率 β\beta ，到这个点时将会有 β\beta 概率继续走，否则 1−β1-\beta 概率随机跳，一般来说 β∈[0.8,0.9]\beta \in [0.8,0.9] (平均 5 到 10 步就跳出去)

此时我们迭代的公式改写成为

rj=∑i→jβridi+(1−β)1Nr_j=\sum_{i\to j}\beta\frac{r_i}{d_i}+(1-\beta)\frac{1}{N}

换句话说，我们设某个大公司 G 提出额矩阵为

G=βM+(1−β)[1N]N∗NG = \beta M +(1-\beta)[\frac{1}{N}]_{N*N}

公式就变成 r=G⋅rr= G \cdot r

应用举例：推荐系统

给你一个二分图，两边分别是用户和关系。例如有以下情况：

zqwg7n.png

现在的目标就是让你确定与点集 QQ 相关性最大的节点

我们采用PageRank来处理，但是我们做一下更改，把随机传送的节点仅限于点集 S=QS = {Q}

伪代码如图：

zq0sC6.png

需要注意到此时 β=A=0.5\beta=\Alpha=0.5

最后 visit_count\text{visit\_count} 最高的节点就是相似度最高的节点。

这是PageRank及其同分异构体

zq0hVA.png

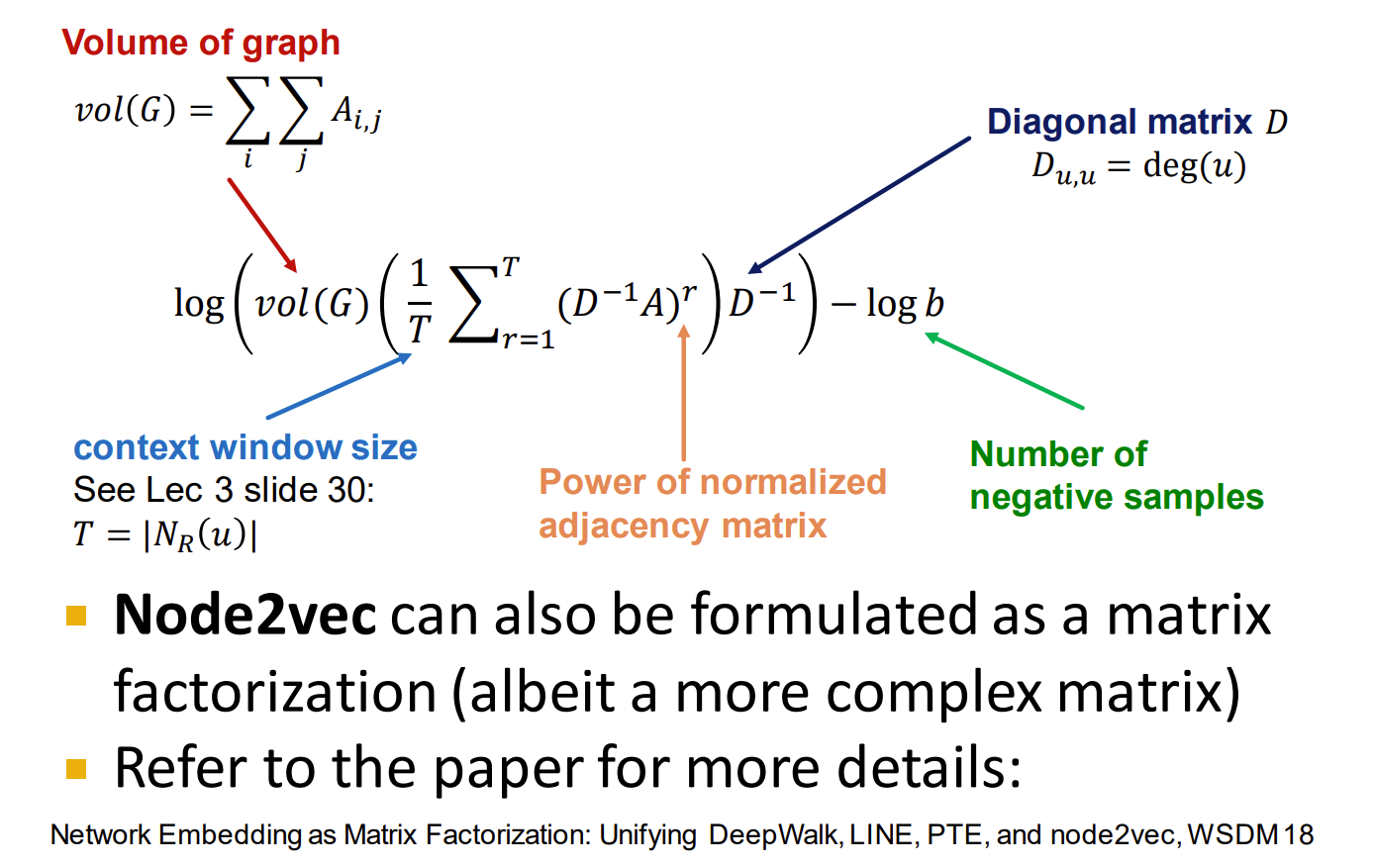
矩阵分解

如果两节点相连，我们就认为相似，此时我们假设一个嵌入矩阵 ZZ ，满足 ZuTZv=Au,vZ_{u}^TZ_{v}=A_{u,v} , AA 为图矩阵，换句话说 A=ZTZA=Z^TZ,显然，这个方法没有降低复杂度。

我们花一种思路，最小化 L2\text{L2} 距离 ,即元素差的平方和， 即min⁡z∣∣A−ZTZ∣∣2\min_{z}\limits||A-Z^TZ||_2 ，实际上用 softmax\text{softmax} 也行

DeepWalk

不想打公式。

zq4m0x.png

缺点

  1. 没法在线，每次加入后得重新计算embedding

  2. 结构相似，例如同样是 K3K_3 ，embedding 后面结果不一样

  3. Cannot utilize node, edge and graph features （没法利用这些东西的特征？）